It is said that “Let no one who is ignorant of geometry enter” was inscribed over the entrance to Plato’s Academy (which lasted for centuries after his death). The Pythagoreans (of Pythagorean theorem fame) made a religion of mathematics; it is rumored that they killed someone who pointed out that the square root of two was what we now call an irrational number (that is, after the decimal point the numbers never end) because the idea didn’t fit in with their model of an ordered, clean, mathematical universe!
Now, while the Greeks had some philosophical tendencies that overlapped with Buddhism (the skeptic founder Pyrrho went to India with Alexander the Great and studied Buddhism, and the Stoics were into non-dualism and had many teachings and attitudes compatible with Buddhism), that is not why I bring up how far back the Western appreciation of mathematics reaches. I do so because mathematics is so foundational to modern scientific thinking. Scientists consider mathematics the language of science. In fact, there are modern scientific “Platonists” like Hawking, Tegmark and Penrose, who have written popular books and are top theoreticians in physics, who believe that we don’t need experimental evidence for their claims about reality. Rather, they believe that mathematics IS reality in its purist form! Mathematics is itself scientific evidence.
So where are they coming from and why do I think you might find mathematics interesting if you are a Buddhist with little or no interest in math or science? Because scientists and mathematicians argue about whether mathematics is something we invented or discovered. Because scientists are blown away by what has been called the unreasonable effectiveness of mathematics in predicting scientific discoveries. But mostly because I see a lot of interesting overlap between what blew the minds of the ancients, both East and West.
Lets look at a Chinese Chan poem and then a Japanese Zen painting to see what I mean. Don’t worry if you hate math. Math is not about numbers. It is about relationships and ideals. I’ll draw you pictures.
Anything that we can experience as existing in time and space (that is, the realm of the senses) is in the realm of the “relative,” and whatever is true regardless of time and space is in the realm of the “absolute.” There is a tension between the relative–the relational, the contingent, the deep and abiding interconnectedness and interaction of what is in time and space–and the absolute. Zen practitioners know I didn’t come up with this terminology. There is an ancient Chinese Chan poem that we chant in some of our services. In Mandarin it is called Cantongqi, in Japanese Sandokai. The poem was written by Shitou Xiqian (Japanese: Sekito Kisen). Shitou lived in 8th century China. The title of the poem is apparently very difficult to translate: “The Identity of Relative and Absolute” is the version we use at Hazy Moon, and I like the kind of mathematical sound and unapologetic nature of “identity.”
Books have been written and series of talks given about this poem. This is one of those places where both science and Zen converge in wonder and profundity. Sages, philosophers and scientists have grappled with this throughout the ages. How do we get something from the ultimate oneness, how is there the illusion of duality if at its heart non-duality must be how it is. For certainly even scientists have some idea of non-duality. Think of the quest to unify the forces of nature. How can there be nature and something else? The identity, or some say the harmony, of the world of the relative and the realm of the absolute is not very amenable to the intellect, to concepts and language, which evolved in the dualistic world of the senses, or even to mathematics, which gets lost in infinities. We can use some ideas from mathematics, at least as metaphors perhaps, even if just to get us started. We’ll do this by looking at the universe embodied in the circle, and to do that, lets look at symmetry and the breaking of symmetry.
There are many types of symmetry. You can see mirror symmetry in the fluke of a whale. The right half of the fluke is the mirror image of the left, and visa versa. That is why the water is so evenly dispersed in the photograph of the fluke. Such symmetry is very functional for the diving whale. An asymmetric fluke would not work as well to stabilize the whale when she dives.

The conservation laws of physics are also defined by symmetry. When we say the total energy of a system is constant, that is, that energy is “conserved,” we are saying the total energy is the same before and after you do something to the system (an experiment, say).
Look at the energy of the system before the experiment, and then close your eyes while somebody else does the experiment. When you look at the total energy of the system (including any added or subtracted, say by heating or cooling during the experiment) when you open your eyes after the experiment is done, you can’t tell there was any change; it passes the “can’t tell” test that defines symmetry.
Actually we can’t measure total energy directly (the slippery nature of energy is another discussion, but even defining, let alone measuring, the total energy is clearly beyond our grasp). We can measure changes in energy. And that will be zero. If you added energy here, some was lost somewhere there. If not, you have some explaining to do. From a scientific viewpoint that can be where the real action is! A discrepancy in energy accounting could be evidence of a new particle that carried away some of the energy you couldn’t account for (this has happened), or even a new law of physics, although it is more likely you just missed something or didn’t take accurate measurements. So you try again, and if the difference remains, and it isn’t carelessness or the lack of sufficiently sensitive instruments, then you really may be on to something new! Why is energy conserved? That’s a bit far afield from this discussion, but I think it has to do with being beginningless, bottomless, endless and uncreated.
The point is, energy is conserved and any discrepancies need to be addressed. The conservation of energy is a form of symmetry.
Let’s look more closely at just what symmetry is by looking at rotational symmetry as an example. If you close your eyes and I rotate an unmarked circle, when you open your eyes and look at the circle you can’t tell that I did anything; you still see a circle, just like before. Nothing about the circle looks different. This “can’t tell” test is a hallmark of symmetry.
The entity we call a circle is an idea. It is empty of “thingness.” A circle is defined as that object that is equally distant at every point from a central point. This distance is the radius of the circle (think about it; it works!). So all it takes is a distance from a point to define a circle. Yet in fact, no ideal circle actually exists. Even the most close to perfect circle you can create in the world of the relative is marred minimally by quantum fluctuations even of you were to design a circle to the precision of the atomic or subatomic scale.
In Japanese Zen calligraphy there are circles called enso. Of course enso are not perfect circles. They are the product of a brain, a hand, paper, ink and a brush. They are in time and space. This is the identity of relative and absolute at play, the absolutely ideal circle without beginning or end and the relative circle existing in time and space.
A perfect circle doesn’t lend itself to creating the universe of the senses, the realm of the relative. The symmetry is too good. But inherent in that circle is everything that ever was and ever could be. We just need to break the symmetry. When the rotational symmetry is broken, we can produce waves, and these waves define particles, the basis of form.
Open up a circle and you break that rotational symmetry and get a different symmetry that is limited as to rotation, but can be repeated as infinite cycles in all directions in space and time. You get the wave. We can derive that mathematically, but let me just show you a picture:
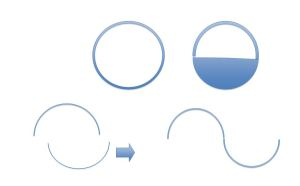
We take a perfect circle and divide it in half. Now there is direction, duality, up and down, top and bottom; if we more the lower half so that the left tip of that lower half meets the right tip of the upper half of the circle and we get a wave.
You can repeat that wave (essentially rotating the circle) without ever needing to stop (mathematically). The circle and the wave both have no beginning and no end.
The wave does have symmetry. You can flip it around the point where the two halves of the circle touch and you get the same wave (passes the can’t tell test). But it isn’t the rotational symmetry of the circle it was derived from, the unbroken circle. We broke the never ending, “absolute” rotational symmetry and found a new, more limited symmetry, the wave, which now brings us to the “relative.”
Mathematically we can sculpt waves. Just like additive sculpting (say in clay) or subtractive sculpting (say in marble), we add and subtract waves to get new waves, even crafting a sharp localized spike. That spike is the particle. The really, really relative, the really, really NOT symmetric!
And hidden in a spike, that particle, there can be countless waves adding and subtracting, creating the spike mathematically.
This is Fourier mathematics, and it is the basis of quantum field theory.
In the circle there is the wave, in the wave the particle, in the particle the wave, in the wave the circle.
We have the identity of the relative and absolute, asymmetry and symmetry, and the particle and wave.

The ancients knew about symmetry and symmetry breaking, circle and waves, the identity relative and absolute. Just look at the Yin Yang symbol! You see circle, and broken circle, wave and particle.

They experienced it in their beings, in their lives. That is what it is really all about.
Now lets expand our look at circles and waves by looking at a Japanese Zen painting
Sengai Gibon (1750-1838) was a Japanese Zen master who was an artist. There are many stories about Sengai. One I particularly like shows his courage and compassion. The Daimyo, the high-ranking Samurai who was the local ruler, loved chrysanthemums. The gardener’s dog destroyed some of his prized blooms and so naturally the gardener needed to die. Sengai leveled the rest of the flowers with is trusty scythe, presenting himself to the Daimyo the next day. Sengai asked to be killed. After all, farmers, who were dying of hunger, were ignored by the Daimyo while pretty plants were valued above a human life.
The Daimyo got the message.
One of Sengai’s most famous works is “Circle Triangle Square.”

There are many interpretations of what this painting is about.
The inscription at the left of the painting alludes to Sengai’s temple, an ancient temple already at that time about 700 years old. It was the first Zen temple in Japan. So maybe the shapes refer to the temple and the pagoda at the temple and some nearby mountain.
Or maybe the inscription is not about the subject of the painting and it is just in effect his signature. Zen masters in Japan and before that China were often identified with and named after their monasteries or the mountains they lived on.
Or maybe the circle is the cushion (zafu) the meditator sits on, the triangle is the mediator with the top point as the head, the solid base of the triangle being the butt and crossed legs. The triangle could be meditator as mountain. The square might be the zabuton, the square pad the zafu sits on (the triangle/meditator/mountain idea was suggested in conversations with sensei Maezen at Hazy Moon).
Lets get Platonic. I would like to interpret the painting geometrically. I have no idea how much geometry Sengai knew. Clearly basic geometric shapes interested him enough to paint them.
So circles are amazing but where do squares and triangles come in? How do they relate to the unwinding of the perfect circle as a wave that we saw in the article “Circle and Wave”?
Lets start with how a square and triangle relate. A square is two triangles.

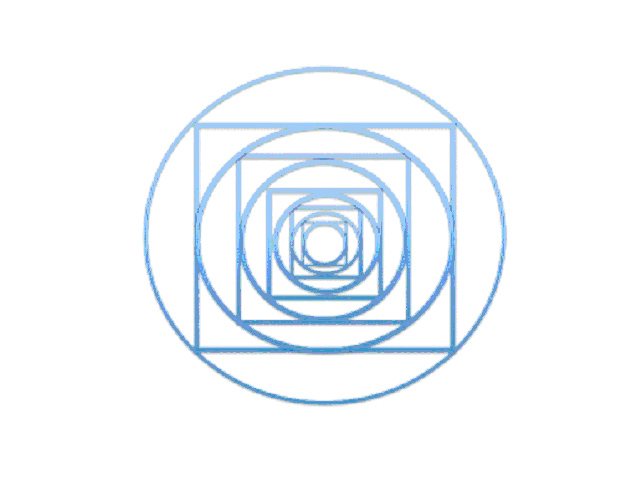
Next, how do circles and squares relate? There are many ways, but here is one I like: every circle precisely defines two squares, each of which intersects with the circle at four points. One square is inside, the other outside the circle. Every square likewise defines exactly two circles, each circle intersecting with the square at four points:

Those then define two larger and smaller squares and circles ad infinitum.
Now, how do circles and triangles relate and how do they make waves? We can think of the circle as a clock face. This time we will think of the radius that defined the circle (that distance that all points were from the center point) as a minute hand, here pictured as arrows. For this illustration the minute hand will go counter-clockwise, starting at the 3 o’clock position (hey, why not?). As we rotate this minute hand radius counterclockwise we will note how high the tip of the arrow is above or below the horizontal line bisecting the circle.
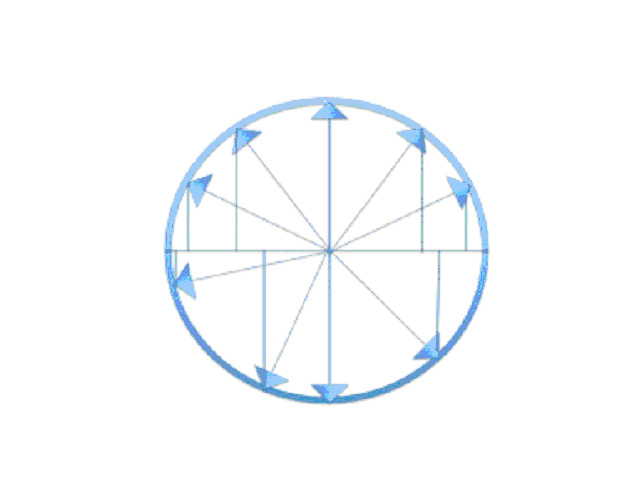
Next let’s put each vertical line (the distance of the radius above or below the horizontal bisecting line) along a new horizontal line, with each clock hour marked, starting at 3 o’clock and going counterclockwise (3 o’clock, 2 o’clock, etc.) around the circle/clock. Even with just a few straight lines we see a wave emerging if we connect the tips of the arrows:
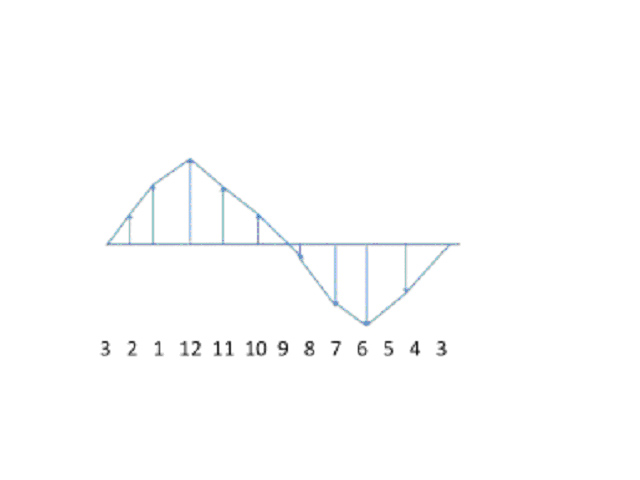
In this figure we placed the vertical lines above and below the horizontal line at their clock positions in the circle as marked on the horizontal line and connected the tips of the arrows with lines and got a rough wave.
If we were to add so many arrows (each a radius of the clock/circle, that is, the distance form the center point that defined the circle) and the resulting vertical lines from the tip of the arrow to the horizontal bisecting line so that the circle is filled with lines and arrows we would get a perfectly smooth wave. In the ideal, mathematically pure case, a perfect wave, unlike the complex messy waves of contingency we see at the beach.
What is this wave?
Each arrow is a radius of that circle. It also is the hypotenuse (the longest side) of a right triangle (And why not? Any line can be turned into a hypotenuse by adding two other lines!).
Here is one radius arrow and the horizontal line isolated (with a line connecting the tip of the arrow to the horizontal) to show that each arrow indeed defines a specific right triangle:
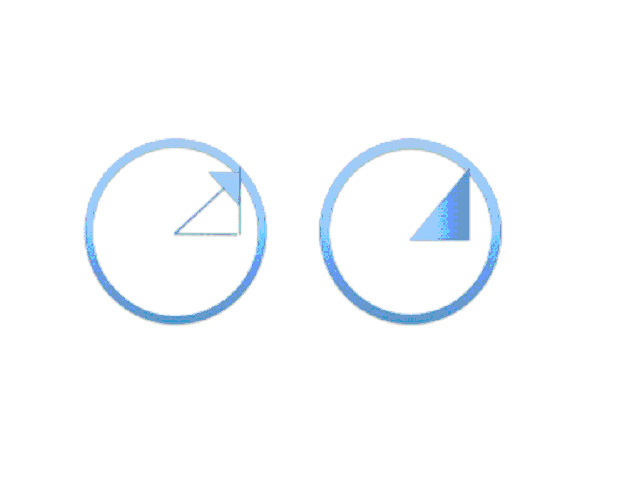
This figure shows one of the triangles defined by the arrow (radius) and the line from the tip of the arrow to the horizontal bisecting line.
Now, lets say the arrow/radius/hypotenuse is one unit. It doesn’t matter one unit of what. A unit could be one inch, one mile, one light year, one unit of 6.753 millimeters, one diameter of an oxygen atom, it doesn’t matter; all are kosher as long as all other measurements that relate to that unit length, say of the other sides of the triangle, are measured in a way that is related to that basic unit (in multiples of inches, of miles, of light years, of 6.753 mm, of diameters of oxygen atoms, etc.).
Then we can define a specific relationship and give it a name: the sine of a right triangle is defined as the length of the side opposite an angle (other than the right angle) over (that is, divided by) the hypotenuse. It is a ratio, so there no need to worry about units of measurement as any units are on the top and bottom of the ratio, so they just cancel. This ratio is just a relationship that always holds because we defined it that way. Since the arrow/hypotenuse/radius here is 1, the denominator of the ratio of the “line across from the angle”/”arrow” relationship (the sine), so the line across from the angle IS the sine for that triangle. After all anything divided by 1 is just that thing.
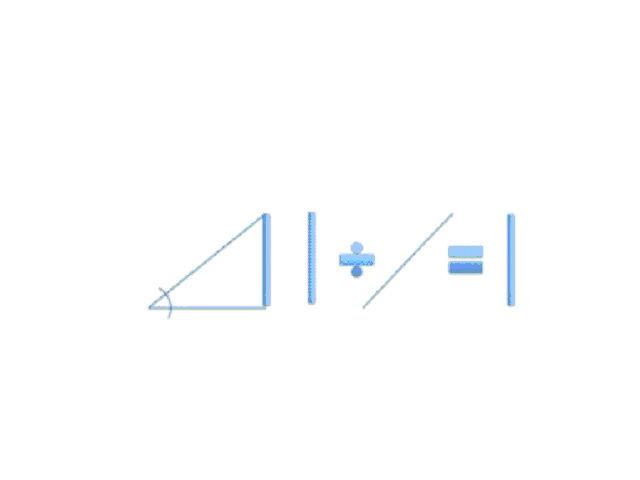
Here we see a right triangle. The thick line is the side across from the angle. The diagonal line is the hypotenuse (the arrow, or radius, in our circle). To the right of the triangle we have the thick line divided by the diagonal hypotenuse (which we defined as being 1 unit long) = the thick line (the thick line divided by 1 = the thick line). The length of that thick line then is the sine of that angle (defined as the side opposite of an angle over the hypotenuse which is 1 unit)
We collected these sides of the triangles, which were the length of the tip of the arrow above or below the horizontal bisecting line, and we created a sine wave! So the triangle sine and the sine wave of the circle are one thing.
Circle, square. Every square defines two circles; every circle defines two squares, without beginning or end.
Square triangle. Two triangles make a square.
Circle triangle. Every circle is made up of the hypotenuse of triangle after triangle, and these have relationships that define waves (we just looked at one such wave, the sine wave). Waves have no beginning or end. We arbitrarily started and stopped at 3 o’clock on the circle. We could have kept going around and around the circle without end, and we could have started anywhere on the circle.
We could have gone in the opposite direction as well. These changes would have defined waves, just not sine waves (e.g. cosine).
And waves, as we have seen add and subtract to form particles. Wave and particle, the quantum conundrum, is then found in Sengai’s art, in the yin yang symbol.
So do you think Sengai had any of this in mind? Did he know trigonometry? Did he intuit that these basic forms could describe all form? That these objects that have no physical existence but are abstractions, the product of mind, empty of substance, are the basis of all we consider substance in our quotidian lives embedded in the senses, the basis of all math and science, all time and space, the absolute inherent in the relative, the relative emerging from the absolute? In Mind?
Is this the dreams stuff is made of? Are these the parameters of the phantoms we chase?
Dogen Zenji:
“Nevertheless this great ocean is neither a circle nor has directions. The wondrous features of this ocean that remain beyond our vision are inexhaustible…. It is just that as far as my vision reaches for the time being, it appears to be a circle.”
__________________________________________________________
Photos courtesy of Susan Levinson
Visit Ralph Shikan Levinson’s website: ZenGut
